Tags
ATM, barium, Bausch & Lomb, Bureau of Standards, flint, glass, Hopewell Observatory, Math, mystery glass, Optics, Schott, Snell's Law, Telescope
Many years ago, the late Bob Bolster, a founding member of Hopewell Observatory and an amazing amateur telescope maker, got hold of a large piece of glass, perhaps World War Two military surplus left over from the old Bureau of Standards.
I have no idea what it is made out of. If Bob had any clue about its composition, he didn’t tell anyone.
Its diameter is 22 inches, and its thickness is about 3.25″. It has a yellowish tint, and it is very, very heavy.
If you didn’t know, telescope lenses (just like binocular or camera lenses) are made from a wide variety of ingredients, carefully selected to refract the various colors of light just so. Almost all glass contains quartz (SiO2), but they can also contain limestone (CaCO3), Boric oxide (B2O3), phosphates, fluorides, lead oxide, and even rare earth elements like lanthanum or thorium. This link will tell you more than you need to know.
If you are making lenses for a large refracting telescope, you need to have two very different types of glass, and you need to know their indices of refraction very precisely, so that you can calculate the the exact curvatures needed so that the color distortions produced by one lens will be mostly canceled out by the other piece(s) of glass. This is not simple! The largest working refractor today is the Yerkes, with a diameter of 40 inches (~1 meter). By comparison, the largest reflecting telescope made with a single piece of glass today is the Subaru on Mauna Kea, with a diameter of 8.2 meters (323 inches).
For a reflecting telescope, one generally doesn’t care very much what the exact composition of the glass might be, as long as it doesn’t expand and contract too much when the temperature rises or falls.
We weren’t quite sure what to do with this heavy disk, but we figured that before either grinding it into a mirror or selling it, we should try to figure out what type of glass it might be.
Several companies that produce optical glass publish catalogs that list all sorts of data, including density and indices of refraction and dispersion.
Some of us Hopewell members used a bathroom scale and tape measures to measure the density. We found that it weighed about 130 pounds. The diameter is 22 inches (55.9 cm) and the thickness is 3 and a quarter inches (8.26 cm). Using the formula for a cylinder, namely V = pi*r2*h, the volume is about 1235 cubic inches or 20,722 cubic centimeters. Using a bathroom scale, we got its weight to be about 130 lbs, or 59 kg (both +/- 1 or 2). It is possible that the scale got confused, since it expects two feet to be placed on it, rather than one large disk of glass.
However, if our measurements are correct, its density is about 2.91 grams per cc, or 1.68 ounces per cubic inches. (We figured that the density might be as low as 2.80 or as high as 3.00 if the scale was a bit off.)
It turns out that there are lots of different types of glass in that range.
Looking through the Schott catalog I saw the following types of glass with densities in that range, but I may have missed a few.
2.86 N-SF5
2.86 M-BAK2
2.89 N-BAF4
2.90 N-SF8
2.90 P-SF8
2.91 N-PSK3
2.92 N-SF15
2.93 P-SF69
2.94 LLF1
2.97 P-SK58A
3.00 N-KZFS5
3.01 P-SK57Q1
By comparison, some of the commonest and cheapest optical glasses are BAK-4 with density 3.05 and BK-7 with density 2.5.
Someone suggested that the glass might contain radioactive thorium. I don’t have a working Geiger counter, but used an iPhone app called GammaPix and it reported no gamma-ray radioactivity at all, and I also found that none of the glasses listed above (as manufactured today by Schott) contain any Uranium, Thorium or Lanthanum (which is used to replace thorium).
So I then rigged up a fixed laser pointer to measure its index of refraction using Snell’s Law, which says
Here is a schematic of my setup:

The fixed angle a I found to be between 50 and 51 degrees by putting my rig on a large mirror and measuring the angle of reflection with a carpentry tool.
And here is what it looked like in practice:
I slid the jig back and forth until I could make it so that the refracted laser beam just barely hit the bottom edge of the glass blank.
I marked where the laser is impinging upon the glass, and I measured the distance d from that spot to the top edge of the glass.
I divided d by the thickness of the glass, in the same units, and found the arc-tangent of that ratio; that is the measure, b, of the angle of refraction.
One generally uses 1.00 for the index of refraction of air (n1). I am calling n2 the index of refraction of the glass. I had never actually done this experiment before; I had only read about doing it.
As you might expect, with such a crude setup, I got a range of answers for the thickness of the glass, and for the distance d. Even angle a was uncertain: somewhere around 49 or 50 degrees. For the angle of refraction, I got answers somewhere between 25.7 and 26.5 degrees.
All of this gave me an index of refraction for this class as being between 1.723 and 1.760.
This gave me a list of quite a few different glasses in several catalogs (two from Schott and one from Bausch & Lomb).
Unfortunately, there is no glass with a density between 2.80 and 3.00 g/cc that has an index of refraction in that range.
None.
So, either we have a disk of unobtanium, or else we did some measurements incorrectly.
I’m guessing it’s not unobtanium.
I’m also guessing the error is probably in our weighing procedure. The bathroom scale we used is not very accurate and probably got confused because the glass doesn’t have two feet.
A suggestion was made that this might be what Bausch and Lomb called Barium Flint, but that has an index of refraction that’s too low, only 1.605.
Mystery is still unsolved.

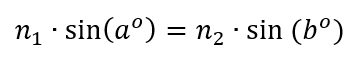

doctor’s office has more appropriate scale
LikeLike
I’ve been in the Tucson astronomy club for many decades and also in the optics industry there. Most all institutions that had connections to astronomy or optics in the 60s got portions of several semi loads of “glass bank glass”, glasses that at one point in the past were considered strategic materials for certain optical designs/systems. There was a wide variety of materials, but almost all was identified in some way. We’re there any markings ar data scribed in the glass? The largest I saw was about 15”, so yours might be a different source.
A co-worker of mine has identified several mystery glasses from an accurate determination of density. Seems like you should be able to get better results w/a more accurate scale. Also many glass types made decades ago are obsolete – my friend has some older glass catalogs that might help you determine what it might be with more accurate numbers. Feel free to drop a line…
LikeLike
I had no idea this was so widespread!
I should’ve realized!
This is basically leftover optics from our military industrial complex, and it was located all over the country!
I’ve looked over this piece of glass pretty thoroughly and IIRC nothing at all was written on it.
Yes, a better weight scale is needed. I haven’t figured out how to carry that off (pun intended). Did I mention that this thing is really heavy? And that it’s under a really heavy Draper-style grinding and polishing machine, also made by Bob Bolster? No can budge either one by myself.
LikeLike