Category Archives: Math

Why Not Show Students the Beauty of Math?

16 Tuesday Oct 2018

Posted by in education, Math, teaching

≈ Leave a comment

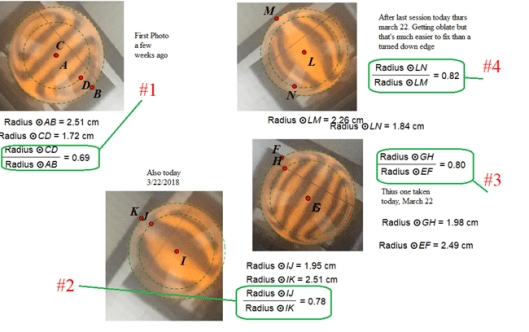
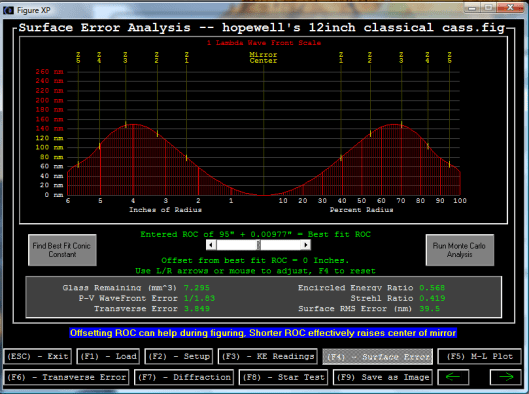
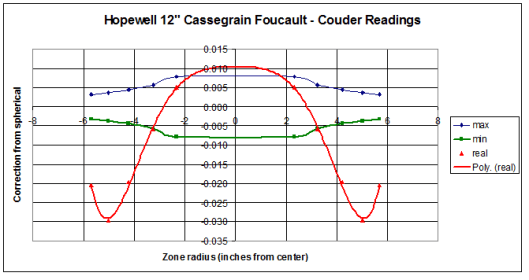
Tags

, , , , , , , , , , ,

When I taught math, I tried to get students to see both the usefulness and beauty of whatever topic we were discussing. The most beautiful mathematical objects I know of are the Mandelbrot and Julia sets, which in my opinion should be brought up whenever one is studying imaginary and complex numbers.

To illustrate what I mean, here are some blown up pieces of the Mandelbrot set. Below,  I’ll explain the very simple algebra that goes into making it.

 

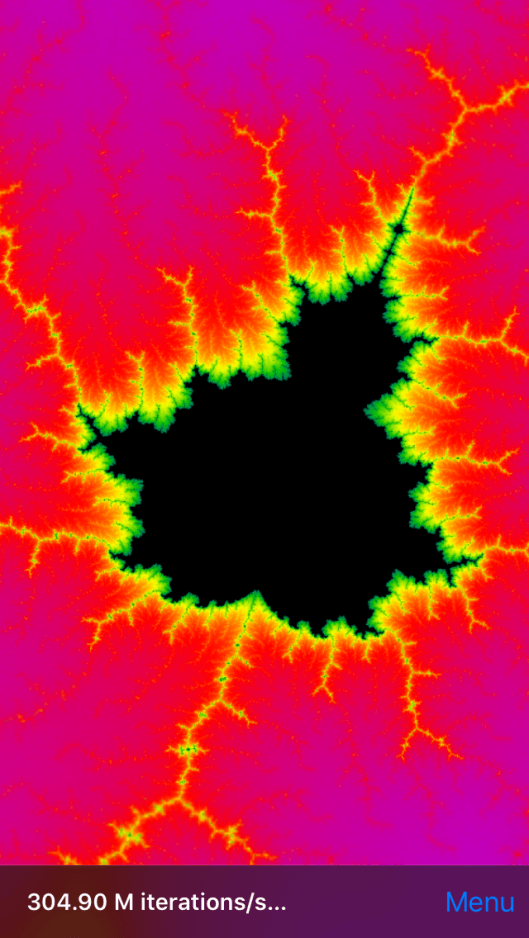
I made these images using an app called FastFractal on my iPhone. The math goes like this:

Normally, you can’t take the square root of a negative number. But let’s pretend that you can, and that the square root of negative one is the imaginary number i. So the square root of -16 is 4i. Furthermore, we can invent complex numbers that have a real part like 2, or 3.1416, or -25/17, or anything else, and an imaginary part like 3i or -0.25i. So 2-3i is a complex number.

Ok so far?

We can add, subtract, multiply and divide real, imaginary and complex numbers if we want, just remembering that we need to add and subtract like terms, so 4+3i cannot be simplified to 7i; it’s already as simple as it gets. Remember that i multiplied by i gives you negative one!

Interesting fact: if you multiply a complex number (say, 4+3i) by its conjugate (namely 4-3i) you get a strictly REAL answer: 25! (Try it, using FOIL if you need to, and remember that i*i=-1!)

Furthermore, let us now pretend that we can place complex numbers on something that looks just like the familiar x-y coordinate plane, only now the x-axis becomes the real axis and the y-axis becomes the imaginary axis. So our complex number 4+3i is located where the Cartesian point (4, 3) would be.

Ok — but what’s the connection to those pretty pictures?

It’s coming, I promise!

Here’s the connection: take any point on the complex plane, in other words, any complex number you wish. Call it z. Then:

(1) Square it.

(2) Add the original complex number z to that result.

(3) See how far the result is from the origin.

(4) Repeat steps 1 – 3 a whole lot of times, always adding the original z.

One of two things will happen:

(A) your result stays close to the origin, OR

(B) it will go far, far away from the origin.

If it stays close to the origin, color the original point black.

If it gets far away, pick some other color.

Then repeat steps 1-4 for the point “right next” to your original complex point z. (Obviously, the phrase “right next to” depends on the scale you are using for your graph, but you probably want fine coverage.)

When you are done, print your picture!

If we start with 4+3i, after one round I get 11+27i. After two rounds I get -604 + 597i, which is very far from the origin, so I’m going to stop here and color it blue. I’ll also decide that every time a result gets into the hundreds after merely two rounds, that point will also be blue.

Now let’s try a complex point much closer to the origin: how about 0.2+0.4i? I tried that a bunch of times and the result seems to converge on about 0.024+0.420i — so I’ll color that point black.

This whole process would of course be very, very tedious to do by hand, but it’s pretty easy to program a graphing calculator to do this for you.

When Benoit Mandelbrot and others first did this set of computations in 1978-1980, and printed the results, they were amazed at its complexity and strange beauty: the border between the points we color black and those we color otherwise is unbelievably complicated, even when you zoom in really, really close. Who woulda thunk that a simple operation with complex numbers, that any high school student in Algebra 2 can do and perform, could produce something so beautiful and weird?

So, why not take a little time in Algebra 2 and have students explore the Mandelbrot set and it’s sister the Julia set? They might just get the idea that math is beautiful!!!

IMG_1735

Math – How Come We Forget So Much of What We Learned in School?

27 Monday Aug 2018

Posted by in astrophysics, education, History, Math, science, teaching, Telescope Making, Uncategorized

≈ Leave a comment

Tags

, , , , , ,

This was a question on  Quora. Here is an answer I wrote:

In the US, judging strictly on what I’ve seen from my time in the classroom as both a student, a teacher, and a visiting mentor of other math teachers, I find that math and science was very often taught as sort of cookbook recipes without any real depth of understanding. The recent National Council of Teachers of Mathematics prescriptions have attempted to correct that, but results have been mixed, and the Common Core has ironically fostered a weird mix of conceptual math marred by teachers being *OBLIGATED* to follow a script, word-for-word, if they want to remain employed. Obviously, if students are really trying to understand WHY a certain mathematical or scientific thing/fact/theorem/theory/law is true, they are going to have questions, and it’s obviously the teacher’s job to figure out how best to answer said questions — which are not likely to have pre-formulated scripts to follow in case they come up — and which are going to take time.

Another thing that is true is that not everything in mathematics has real-world applications in every single person’s life. I taught a good bit of computer programming (aka ‘coding’ today), geometry, arithmetic, probability, algebra, statistics, and conic sections, and in fact I use a LOT of that every week fabricating telescope mirrors to amazing levels of precision, by hand, not for a living, but because I find telescope-making to be a lot of fun and good mental, aesthetic, manual, and physical exercise. But I’m a pretty rare exception!

Most people obviously don’t dabble in math and physics and optics like I do, nor should they!

In fact, I have made it a point to ask professional scientists and engineers that I meet if they actually use, on their jobs, all the calculus that they learned back in HS and college. So far, I think my count is several dozen “Noes” and only one definite “Yes” – and the latter was an actual rocket scientist / engineer and MIT grad and pro-am astronomer (and wonderful, funny, smart person) who deals/dealt with orbital rocket trajectories. (IIRC).

In France, when I went to school there 50 years ago and in my experience tutoring some kids at the fully-French Lycee Rochambeau near Washington, DC, is that they go very deeply into various topics in math, and the sequence of topics is very carefully thought out for each year for each kid in the entire nation (with varying levels of depth depending on what sort of track that the students elected to go into (say, languages/literature, pure math, or applied sciences, etc), but the kids were essentially obligated to accept certain ideas as factual givens and then work out more and more difficult problems that dealt with those particular givens. No questions allowed on where the givens came from, except to note the name of the long-dead classical Greek, French, Italian or German savant whose name is associated with it.

As an American kid who was mostly taught in American schools, but who also took 2 full years of the French system (half a year each of neuvieme, septieme, premiere, terminale, and then passed the baccalaureat in what they called at the time mathematiques elementaires, I found the choice of topics [eg ‘casting out nines’ and barycenters and non-orthogonal coordinate systems] in France rather strange. Interesting topics perhaps, but strange. And not necessarily any more related to the real world than what we teach here in the US.

Over in France, however, intellectuals are (mostly) respected, even revered, and of all the various academic strands, pure math has the highest level of respect. So people over there tend to be proud of however far they got in mathematics, and what they remember. Discourse in French tends to be extremely logical and clear in a way that I cannot imagine happening here in the public sphere.

So to sum up:

(a) most people never learned all that much math better than what was required to pass the test;

(b) only a very few geeky students like myself were motivated to ask ‘why’;

(c) most people don’t use all that much math in their real lives in the first place.

 

 

Quantifying Progress in the Fight Against Turned Down Edge

27 Tuesday Mar 2018

Posted by in astronomy, Math, Optics, Telescope Making, Uncategorized

≈ Leave a comment

Tags

, ,

By Guy Brandenburg

3/27/2017

I describe here an attempt to quantify progress (or lack thereof) in the removal of the classic, and dreaded, turned-down edge (TDE) present on a 16.5” Newtonian glass mirror blank that I have been trying to “figure” for some years.  The figuring process means changing a piece of glass that approximates a small section sliced out of a large hollow sphere, into a highly-accurate paraboloid — with the required level of accuracy being measured in nanometers.

 

Many amateur and professional telescope makers have maintained that you can only fix figuring errors if you can measure them. Not being able to get good, repeatable measurements of the TDE on my mirror, I had been sort of floundering, failing to get rid of the TDE even after YEARS of work (off and on; mostly off). So a decision was made to try to quantify things.

 

We recently had some success in matching computer-generated Ronchi images of theoretically-perfect mirrors with photos taken of works in progress, simply by cutting and pasting – which has been recommended by Mel Bartels in particular for quite some time. For the first time, I got the hang of it, and we were able to help a first-timer (Mike L) to figure a 10” plate glass f/5.4 mirror only ¾” thick to just about exactly ¼ lambda, according to our combined, repeated, careful measurements on a mirror that was cooled both by immersion in a room-temperature water bath and by sitting in a closet in the very same testing room for an entire weekend.

 

Prior to this experiment, I had been taking short videos of the entire mirror, moving the ronchi grating back and forth across the center of curvature. These videos reveal and record a lot of qualitative information about the mirror, including vocal commentary, but I found it impossible to transfer the images to my laptop for closer analysis until I got home, across town, which meant that the turn-around time after testing a mirror was much too long to be of any use. I had tried quite a large number of various strokes suggested by others, by our reading various ATM manuals, and by just thinking; but the very serious TDE on this (for me, relatively ambitious) project never seemed to get any better.

 

I simply gave up on imaging via video clips, since they were too hard to manipulate or measure on my phone, and which required too much bandwidth to send to my laptop until I got home. This time, I took Ronchi still-images on my cell phone, between 0.2 and 0.5 inches outside of the center of curvature.

guys 16 perfect

(My experience has been generally easier to discern defects in a Ronchigram when the lines curve outwards at the top and bottom, which would mean the test grating is  OUTSIDE the COC of a partly-parabolized mirror, as you see on the left in the black-and-white image above. However, when the lines curve inwards at the top and bottom, like the images in the center and to the right, then many serious defects remain hidden. quantify TDE

Procedure:

A standard 100 LPI grating from Willmann-Bell and a yellow LED were used, on an XYZ stage partly fabricated by me and placed exactly twice the focal length from the primary. Images were taken with an iPhone 6, shooting images zoomed in as much as possible. An attempt was made to have matching ronchigrams, i.e., with the same number of vertical lines showing.

 

(This was a weak point of the experiment. For one, it’s hard to hold cell phone steady enough, and an observer will notice that the images do NOT have exactly the same number of lines. That’s because I did not have a printout of the previous image right in front of me to make comparisons to. All that needs to be fixed in subsequent iterations. Also, other imaging devices need to be tried, as well.)

 

I was in fact able to email individual photograph frames to my laptop at the lab. After downloading the clearest images to my laptop, I used plain old MS Windows Paint to shrink and crop the useful portion of the picture, and then pasted the result into a Geometry software (Geometer.s Sketchpad, or GSP) that I was already familiar with. GSP was then used to draw a circle around the circumference of the image of the nearly-perfectly-circular glass disk, adjusting this as well as possible. This process automatically generated the center of the disk. Using that center, a second, and smaller, circle was drawn whose circumference was placed at the location along the ronchi lines where they appeared to begin to turn outwards. GSP was then  to measure directly the radii of the two circles and to compute their ratio.

 

A final ratio of 0.7, just to pick a number that is easy to compute, means that just about half of the area of the mirror is covered by a wide rolled-down edge, since the ratio of areas is equal to the square of the ratio of the respective radii, and 0.7 squared is 0.49, or 49%.

 

In the diagram above, the images go in chronological order but COUNTER-clockwise, from upper left (labeled #1), which was made in mid- or early March, through the next three images, all taken on March 22. In between each image, various strokes were employed in figuring sessions for anywhere between 15-20 minutes to attempt to fix the TDE. All the figuring sessions involved sub-diameter laps anywhere from 8 to 12 inches in diameter that had been warm-pressed upon the mirror. The strokes were both forward and back and incorporated enough of a ‘W’ stroke to cover the entire mirror, using cerium oxide on either tempered burgundy or Acculap pitch, depending. The edge of the tool was allowed to go up to the edge of the mirror, +/- maybe 5 mm. The goal was simply to wear down the glass in the center until it caught up with the amount that the edge had been worn down. None of the laps seemed to have full contact with the mirror out to the very edge; thus the end of the stroke was NOT at the edge of the mirror.

 

You will notice that these ratios, circled in green, seem to increase monotonically from 69% to 80%, which is gratifying: if this real, then the fraction of the mirror that is NOT covered by TDE has gone from about 47% to about 67%, as you can see here. (Note: in figure #1, the large circle was denoted circle AB, and the smaller circle was denoted circle CD. I know that points A and C are not identical, but they are rather close; that error will be fixed in subsequent iterations.)

However: the key question is: IS THIS REAL? Or am I merely fooling myself?

I don’t know yet.

I certainly hope it is real.

But it needs to be checked with subsequent investigation.

My attempt at limiting my own subjectivity or wishful thinking was to try to draw the circles at the place where the more-or-less vertical lines began turning outwards. Hopefully that location really corresponded to the place where the turned/rolled edge began. However, it is entirely possible that the precise apparent location of the beginning of the TDE very much depends on exactly how many lines appear in the Ronchigram, thus, precisely how far from the COC the grating is located.

Unfortunately, often times I have to dismantle the entire apparatus, because we have to close up shop for the night, or somebody else needs to use the tester on another mirror. Thus, it is nearly impossible to ensure that the measurement apparatus remains undisturbed.

My next steps, I think, are these:

  1. Have a separate, and very simple ronchi apparatus that just consists of a grating and a light.
  2. Have previous images right in front of me as I prepare to take the next Ronchigrams, so that I can match the number of lines visible.
  3. Perhaps I should take a series of said standardized ronchigrams both inside and outside of COC with, say, 5 lines visible. I should also take some ronchigrams that might accentuate and expose any possible astigmatism; that is, very close to the COC. Any Ronchi lines that resemble the letters S, Z, J, U, or N would be very bad news.
  4. Attempt to attach a cheap video camera with built-in LED, Ronchi grating, and a suitable lens to make steadier images free from hand wobbles.

I would like to thank Isaac and Elias Applebaum for their diligent and noted explorations in solving a similar question relating to fixing or preventing TDE. That STEM project won them a number of well-deserved awards.

 

 

A 6″ Dob for Young Relatives

31 Wednesday Jan 2018

Posted by in astronomy, Math, Optics, Telescope Making, Uncategorized

≈ Leave a comment

I just finished a 6″ f/8 Dobsonian telescope as a gift for my great-nephews, one of whom I discovered is VERY interested in astronomy and happens to live in a place with pretty dark skies – about the middle of Maryland’s Eastern Shore. The mirror is excellent, and the mechanical parts all work very well — in my opinion. Let’s see what the recipients think.

I finally succeeded in putting in the mirror yesterday afternoon in a very stiff and cold wind right outside my house, estimating where the mirror should go by aiming at a distant chimney. This takes patience because it’s trial-and-error, no matter how much you calculate beforehand!

Later that evening, after the nearly-full Blue Moon came over the trees at DC’s Chevy Chase Community Center where we have our telescope-making classes, fellow ATMer and all-around interesting person Jim Kaiser helped me collimate it by pointing the scope at the illuminated curtains in the windows of the CCCC. We then verified that the Moon actually did come to a focus with the eyepiece nearly all the way screwed in. If you want to focus on closer things than the Moon or galaxies, you need to screw the eyepiece out towards you, the observer in the cheap but effective helical focuser that was lying around the shop.

This scope incorporates a couple of innovations by me, and a bit of artistic whimsy.

First small innovation: I made the secondary diagonal mirror holder so that no tools are needed at all: you just rotate the part holding the elliptical mirror and turn a little thumbscrew to collimate it quickly and easily, while you watch. Here is a sketch of how I made it.new type of secondary holder

 

Second innovation can be seen near my right hand (to your left) atop the cradle: two 1/4″-20 machine screws with simple homemade knobs on top, going through threaded inserts (T-nuts would work too), which push against a piece of lumber in the shape of prism with an isosceles right triangle at each end. I call this the tube brake, which can be applied or released quite easily, whenever needed. Small springs (almost impossible to see in this photo) pull this brake up against the corner of the tube, while the machine screws press it down. If you want to change the position of the eyepiece because a taller or shorter person has arrived, no problem. A few CCW turns of the wooden knobs releases the brake, you rotate the tube to the desired position, and then you lock it down again with a few clockwise turns. If you add or remove a heavy eyepiece or a finder or whatever, same procedure, except this time you can slide the scope up and down inside the cradle.

The artistic whimsy is partly seen in a photo Jim took of me after we got it collimated but before we rushed back inside: lots of colors, thanks to several tons of paint cans salvaged by fellow ATMer Bill Rohrer from being thrown away by a third party who lost his warehouse lease, and also because smurf blue is the favorite color of one of the boys. The altitude bearing is made out of the Corian countertop that my wife and I got rid of a few months ago when we had our kitchen remodeled. (30 years ago we did it ourselves, mostly. This time we hired professionals. They are SOO much faster and better at this than us!)

So that my young relatives can keep this thing looking good, they also get four or five quart or pint cans of paint – the ones I used on the scope. Free, of course. The more we get rid of put to use, the better. They can repaint anything that gets scratched, you see?IMG_9416

You can also see some wood-cutting fun above and below. This retired geometry teacher had a lot of fun figuring out how to lay out and cut out stars with 5, 6, and 7 points, as well as a crescent moon and a representation of Saturn seen with its rings edge-on. I guess you could show Saturn’s rings a 30 to 45 degrees to the viewer, if you instead carved it out of solid wood or did wood burning, but I just had a hand-held jigsaw and a Dremel knockoff. And plus, this is supposed to be a scope that is USED rather than just admired for its artsy parts.

I designed what I wanted onto two sheets of paper and then taped them to the plywood. This worked, but it wasn’t the most wonderful plywood, so on many of the pull strokes, the wood splintered a bit. So that side got to face inside.. Painting all those little nooks and crannies was tough!

design artsy astro cutouts

(The purpose of the cut-outs was simply to make the telescope lighter. It’s got a very heavy and sturdy base. Each square inch of plywood removed saves about 7 grams. Also, more holes means more hand-holds!)

 

 

Trying to Test a 50-year-old Cassegran Telescope

07 Thursday Sep 2017

Posted by in astronomy, flat, Hopewell Observatorry, Math, science, Telescope Making

≈ Leave a comment

Tags

, , , , , , , , , , , , , , , , , , ,

We at the Hopewell Observatory have had a classical 12″ Cassegrain optical tube and optics that were manufactured about 50 years ago.; They were originally mounted on an Ealing mount for the University of Maryland, but UMd at some point discarded it, and the whole setup eventually made its way to us (long before my time with the observatory).

 

The optics were seen by my predecessors as being very disappointing. At one point, a cardboard mask was made to reduce the optics to about a 10″ diameter, but that apparently didn’t help much. The OTA was replaced with an orange-tube Celestron 14″ Schmidt-Cassegrain telescope on the same extremely-beefy Ealing mount, and it all works reasonably well.

 

Recently, I was asked to check out the optics on this original classical Cassegrain telescope, which is supposed to have a parabolic primary and a hyperbolic secondary. I did Ronchi testing, Couder-Foucault zonal testing, and double-pass autocollimation testing, and I found that the primary is way over-corrected, veering into hyperbolic territory. In fact, Figure XP claims that the conic section of best fit has a Schwartzschild constant of about -1.1, but if it is supposed to be parabolic, then it has a wavefront error of about 5/9, which is not good at all.

Here are the results of the testing, if you care to look. The first graph was produced by a program called FigureXP from my six sets of readings:

figure xp on the 12 inch cass

my graph of 12 inch cass readings

I have not yet tested the secondary or been successful at running a test of the whole telescope with an artificial star. For the indoor star test, it appears that it only comes to a focus maybe a meter or two behind the primary! Unfortunately, the Chevy Chase Community Center where we have our workshop closes up tight by 10 pm on weekdays and the staff starts reminding us of that at about 9:15 pm. Setting up the entire indoor star-testing rig, which involves both red and green lasers bouncing off known optical flat mirrors seven times across a 60-foot-long room in order to get sufficient separation for a valid star test, and moving two very heavy tables into said room, and then putting it all away when we are done, because all sorts of other activities take place in that room. So we ran out of time on Tuesday the 5th.

A couple of people (including Michael Chesnes and Dave Groski) have suggested that this might not be a ‘classical Cassegrain’ – which is a telescope that has a concave, parabolic primary mirror and a convex, hyperbolic secondary. Instead, it might be intended to be a Ritchey-Chretien, which has both mirrors hyperbolic. We have not tried removing the secondary yet, and testing it involves finding a known spherical mirror and cutting a hole in its center, and aligning both mirrors so that the hyperboloid and the sphere have the exact same center. (You may recall that hyperboloids have two focal points, much like ellipses do.)

Here is a diagram and explanation of that test, by Vladimir Sacek at http://www.telescope-optics.net/hindle_sphere_test.htm

hindle sphere test

FIGURE 56: The Hindle sphere test setup: light source is at the far focus (FF) of the convex surface of the radius of curvature RC and eccentricity ε, and Hindle sphere center of curvature coincides with its near focus (NF). Far focus is at a distance A=RC/(1-ε) from convex surface, and the radius of curvature (RS) of the Hindle sphere is a sum of the mirror separation and near focus (NF) distance (absolute values), with the latter given by B=RC/(1+ε). Thus, the mirrorseparation equals RS-B. The only requirement for the sphere radius of curvature RS is to be sufficiently smaller than the sum of near and far focus distance to make the final focus accessible. Needed minimum sphere diameter is larger than the effective test surface diameter by a factor of RS/B. Clearly, Hindle test is limited to surfaces with usable far focus, which eliminates sphere (ε=0, near and far focus coinciding), prolate ellipsoids (1>ε>0, near and far foci on the same, concave side of the surface), paraboloid (ε=1, far focus at infinity) and hyperboloids close enough to a paraboloid to result in an impractically distant far focus.

We discovered that the telescope had a very interesting DC motor – cum – potentiometer assembly to help in moving the secondary mirror in and out, for focusing and such. We know that it’s a 12-volt DC motor, but have not yet had luck tracking down any specifications on that motor from the company that is the legatee of the original manufacturer.

Here are some images of that part:

An Eclipse Seen in Wyoming

27 Sunday Aug 2017

Posted by in astronomy, astrophysics, Math, nature, Telescope Making

≈ Leave a comment

Tags

, , , , , , , , ,

I was fortunate enough to have the time and cash to go to Wyoming for the August 21 eclipse. It was truly wonderful,. in large part due to the fact that I had made a 6″ diameter, f/8 Dob-Newt travel telescope that could play three roles: as an unfiltered projection scope onto a manila folder before and after totality; with a stopped-down Baader solar filter during and after totality; and with no filter at all during the two minutes or so of totality.

No photographic image that I have so far seen comes anywhere near the incredible details that I was able to see during those short two minutes.

Here is my not-very-expert drawing of what I recall seeing:

solar eclipse

The red rim on the upper left is the ‘flash spectrum’, or chromosphere. It was only visible for a few seconds at the very beginning of the eclipse. The corona is the white fuzzy lines, but my drawing doesn’t do them justice. On the bottom, and on the right, are some amazing solar prominences — something that I don’t recall having seen in 1994, my first successful solar eclipse. The bottom one might not have been quite that large, but it really got my attention.

Here are a few photos I took before and after totality:

I started planning this expedition over a year ago, and hoped to attend the Astronomical League meeting in Casper, WY. I quickly found that there were absolutely no rooms to be had there, even a year in advance.

Wyoming has fewer people than my home town (Washington DC), and not many populated places in the path of totality. However, I did find a motel in tiny Lander, Wyoming, very close to the southern edge — a location that I had previously found to be very good for viewing eclipses. One of the fellows in our telescope-making workshop, Oscar O (an actual PhD solar astrophysicist) decided he would bring some family and friends along and camp there to view it with me. So he did (see the group photo).

The night before, we went to a site near Fossil Hill, WY to look at stars. The Milky Way was amazing, stretching from northern to southern horizon, and the sky was very, very dark. We met a baking-soda miner (actually, a trona miner) and his 10-year-old daughter; she had a great time aiming my telescope, via Telrad, at interesting formations in the Milky Way. My friends from DC whipped up an amazing dinner on their tiny camp stove. There were LOTS of people camping in the back country there; I bet most of them were there to view the eclipse!

On the eve and morning of the eclipse, after consulting various weather ‘products’, we decided that the predicted clouds in Lander itself would be a problem. (I had been clouded out before, with my wife and children, back in 1991, in Mexico! It really spoils the experience, I assure you!)

So we drove north and west, through the Wind River Indian Reservation, and picked a spot just east of the tiny town of Dubois at a pulloff for a local fish hatchery. Along the drive to that location, we saw lots of folks had set up camp for the event at various pulloffs and driveways to nowhere. (If you didn’t know, Wyoming is mostly devoid of people, but has lots of fields and barbed wire fence. Many of those fields have driveways leading to some sort of gate, most of which are probably used at least three times every decade, if you get my drift….)

Not only is Wyoming largely empty (of people), but the path of totality in the United States was so long that I estimated that if the ENTIRE population of the USA were to decide to go view the eclipse, and somehow could magically spread themselves out evenly over the 70-mile-wide, and 3000-mile-long, path on dry land, that there would only be about 3 people per acre!

Here’s the math: 70 miles times 3000 miles is 210,000 square miles. The population of the USA is about 330,000,000. Divide the population by the area, and you get about 1600 people per square mile. But there are 640 acres in a square mile, so if you divide 1600 by 640, you get less than 3 people per acre, or 3 people on a football field (either NFL or FIFA; it doesn’t matter which).

(…looking to the future, the next decent eclipse doesn’t seem to occur anywhere in this hemisphere until 2024, when it will cross from Texas to Maine…)

As you can see from my photos, the little travel scope I made, called Guy’s Penny Tube-O III, performed very well. Before and after totality, we used it both for solar projection onto a manila folder, through the eyepiece. I also had fashioned a stopped-down solar filter with a different piece of cardboard and a small piece of Baader Solar Film. With both methods, we could clearly see a whole slew of sunspots, in great detail (umbra and penumbra) as well as the moon slowly slipping across the disk of the sun. Having the sunspots as ‘landmarks’ helped us to watch the progress!

Then, during totality, after the end of Baily’s Beads and the Diamond Ring, I took off the filter and re-adjusted the focus slightly, and was treated to the most amazing sight – a total eclipse, with coronal streamers to the left and right; the ‘flash spectrum’ appearing and winking out on the upper left-hand quadrant (iirc); and numerous solar flares/prominences.

I got generous and allowed a few other people to look, but only for a few seconds each! Time was precious, and I had spent so much work (and airfare) building, and re-building, and transporting that telescope there!

Planets? I didn’t see any, but others did. Apparently Regulus was right next to the Sun, but I wasn’t paying attention.

The corona and solar flares were much, much more pronounced than I recall from 1994.

That afternoon, the town of Lander had the largest traffic jam they had ever had, according to locals I talked to. Driving out of there on that afternoon was apparently kind of a nightmare: the state had received a million or so visitors, roughly double its normal population, and there just aren’t that many roads. I chose to spend the night in Lander and visited from friends I had gotten to know, who are now living in Boulder, on the night after that. Unfortunately, on that next day, I got a speeding ticket and a citation for reckless driving (I was guilty as hell!) for being too risky and going too fast on route 287, trying to pass a bunch of cars that I thought were going too slow…

When I did fly out from Denver, on Wednesday, all the various inspections of my very-suspicious-looking and very-heavy luggage caused me to miss my flight, so I went on standby. It wasn’t too bad, and I was only a few hours later than I had originally planned. And my lost suitcase was delivered to my door the next day, so that was good.

I am now in the process of making this travel scope lighter. I have removed the roller-skate wheels and replaced them with small posts, saving several pounds. I have begun using a mill to remove a lot of the metal from the struts. And I will also fabricate some sacks that I can fill with local rocks, instead of using the heavy and carefully machined counterweights! (Rocks are free, gut going over 50 pounds in your luggage can be VERY expensive!)

 

By the way: unless you like to travel with no luggage at all, NEVER use Spirit Airlines! They may be a few dollars cheaper, but they will even charge you for a carry-on bag! What’s next? Charging you for oxygen?

 

 

Only 15 Types of Plane-Tiling Convex Pentagons Exist

15 Saturday Jul 2017

Posted by in Math

≈ Leave a comment

Tags

, , ,

It has just been proven that only 15 types of convex pentagons exist that can tile the plane. Which implies that there just might be a single polygon (almost undoubtedly concave) that can tile the plane in a non-periodic manner (as do Penrose tiles; but PTs require two different figures, not a single figure).

(If you’ve ever played with regular pentagons, you have discovered that they can’t tile the plane without gaps or overlapping. The pentagons referred to in this proof are NOT regular. Here is one such example, taken from the article:)

a tessellation with pentagons

You can see many of the details at the following link.

 

The Mathematics of George Washington

24 Friday Feb 2017

Posted by in History, Math, Uncategorized

≈ 2 Comments

Tags

, , ,

I recently learned some things about how the young George Washington did math, including surveying. Mathematician and historian V. Frederick  Rickey gave a talk 2 nights ago at the Mathematical Association of America here in DC, based on his study of GW’s “cypher books”, and I’d like to share a few things I learned.

(1) The young George appears to have used no trigonometry at all when finding areas of plots of land that he surveyed. Instead, he would ‘plat’ it very carefully, on paper, making an accurate scale drawing with the correct angles and lengths, and then would divide it up into triangles on the paper. To find the areas of those triangles, he would use some sort of a right-angle device, found and drew the altitude, and then multiplied half the base times the height (or altitude). No law of cosines or sines as we teach students today.

(2) He was given formulas for the volumes of spheroids and barrels, apparently without any derivation or justification that they were correct, to hold so many gallons of wine or of beer. (You probably wouldn’t guess that you had to leave extra room for the ‘head’ on the beer.) Rickey has not found the original source for those formulas, but using calculus and the identity pi = 22/7, he showed that they were absolutely correct.

(3) GW was a very early adopter of decimals in America.

(4 ) This last one puzzled me quite a bit. It’s supposed to be a protractor, but it only gives approximations to those angles. The results are within 1 degree, which I guess might be OK for some uses. I used the law of cosines to convince myself that they were almost all a little off. Here’s an accurate diagram, with angle measurements, that I made with Geometer’s Sketchpad.

His method was to lay out on paper a segment 60 units long (OB) and then to construct a sixth-of-a-circle with center B, passing through O and G (in green). Then he drew five more arcs, each with its center at O, going through the poitns marked as 10, 20, 30, 40, and 50 units from O. The claim is then that angle ABO would be 10 degrees. It’s not. It’s only 9.56 degrees.

Sex and Math: The Zero to Two Percent of Our Actual Lives That Rules Our Lives

01 Thursday Sep 2016

Posted by in Math, science, Uncategorized

≈ 1 Comment

Tags

, , , , ,

Someone (probably Louis CK) pointed out that even though we all obsess about sex (and being attractive to the persons with whom we long to have sex), it’s actually a very, very tiny part of one’s actual (as opposed to our wishful) life.
[Of course, any species that survives needs to have a strong drive for procreation, or they won’t leave enough offspring behind to carry on. (Just ask pandas what happens when they seemingly couldn’t care less… They are, if you hadn’t noticed, nearly extinct in the wild. Rats, rabbits, ants and cockroaches survive by being unbelievably fertile — and sneaky.]
Let’s try to do some math on this.
Have you ever tried figuring out what percent of your entire life has consisted of you actually making love (having sex) with another person?
I am not counting masturbation here because
  • I don’t trust any data on this, even Masters and Johnson, so any guesses on my part would be just that
  • I’m only talking about having sex with another person, either Penis-In-Vagina or any other sort of sexual activity, which I am not about to list here —  use your own imagination if you want to. 
  • And no, I’m not going to tell you anything about my own habits or those of anybody else I know. However, if you want to tally up your OWN time doing ‘that’, feel free.
 
Let’s look at the high end of the spectrum of those having lots of sex first.
My guess is, based on observations of personal experience and what I’ve observed with people I knew well:  that only with the very horniest newly-weds or with a couple who have just entered a super-sensual, brand-new sexual relationship,  time would a couple be spending, say, as much as four hours a day actually’doing it’. Why? For one thing, sex is exhausting. Also, the tissues involved are delicate and can only take so much rubbing, no matter how well lubricated they might be. Plus the couple need to sleep, eat, wash, and most likely do something productive like going to school or work.
That very high figure for someone getting a HUGE amount of nookie is 4 hours  out of 24 hours in a day, or 1/6, which is about 17% of the time. Let me repeat: that’s extraordinarily high, and from my own observations (thin walls allow one to hear… and so on) only seems to last for the first few weeks, because then they get sore, exhausted, sated, and somewhat jaded.
After that, they’d be lucky to be ‘doing it’ for an hour or two a day, which is between about 4 and 8% of the time.
But let’s compare that to the rest of their lives for this remarkably horny and lucky couple… Let’s suppose that they are 20 years old, and let’s suppose that they each had sex a few times in high school and after (college, military, working, whatever, and I’m making no assumptions about whom they are doing this with). Maybe they got laid 2 – 3 times a week from age 16, at about an hour each time (girls, feel free to scoff at my suggestion that a typical male teenager can actually last that long) plus, now that they are not living at parents’ home any more, they have had several tumultuous, sexy relationships one after the next, each time spending an average of 2 hours actively ‘doing it’ each 24-hour period, for the last two full years.
So let’s make that say 6 hours a week for 2 years plus 28 hours a week for the last 2 years – and these people are those who are towards the very far right hand end of the frequency curve distribution. I don’t know whether the distribution of ‘nookie-hours’ if graphed, is ‘normal’ or ‘skewed’one way or the other. But in any case, most people ‘get’ a lot less sex than this. In fact, when I was in high school and college, the vast majority of my (male and female) friends my age or younger were virgins. No, I’m not going to tell you what age or to whom I lost my virginity. I will keep my fond memories to myself, and hope you will do likewise.
Here’s the arithmetic:
Denominator (total hours lived) for this very lucky pair of 20-year olds: 24 hours per day time 365. days per year times 20 years old equals 175,200 hours total that they have lived so far. (D)
 
Numerator ( total hours having sex with another person since they were born) Assuming this very sexually active couple who have sex 6 hours a week times 104 weeks (two years from ages 16 – 18) plus 28 hours a week times 104 weeks (two more years, aged 18 – 20) equals 3,536 hours having sex, grand total, (N)
 
I used a calculator to divide N by D and I get about .02, or two percent of their life so far. That’s tops.Two percent of their life.
I suppose it is theoretically possible that a married couple of 60 years, at age 75, has been actively having sex a full hour every single day of their married life (since age 15). Extremely rare, I know… But for this tiny handful of  extraordinarily horny, happy, healthy and lucky people, I get a grand total of 1/30 of their life, or a tad more than 3%. And I bet that you could probably hold a nice party for every single one of these lucky 75-year-old living couples — from all over the world — in the cafeteria of the elementary school nearest my house. Not sure how much standing room there would be, but this is out of our current world population of over 6 billion people. So they are outliers of outliers of outliers.
The vast majority of people would have much, much less sex than that, I predict with confidence.
Additionally: a good number of people die before losing their virginity. I have no idea what percentage do, but during the old days, it was probably well over half  of them, infant mortality rates being what they were — and I’m assuming that most of those babies and children who died at very early ages from disease, murder or accidents weren’t being sexually abused during their short, sad lives… Many soldiers die in combat having had sex perhaps 0 to 6 times in their entire lives, if I can trust various memoirs I’ve read by veterans of various wars…
So that’s the far left hand end of the ‘bell-shaped’ curve: 0%.
While there are a tiny handful or two-to-three percenters out there, I would bet (if we could test it somehow) that over 99.99% of the population has sex, on average, between ZERO and TWO percent of our entire lives.
But, oh, how we obsess over ‘it’!!